Martes 01 de Noviembre del 2016
Clase#4
Resultado:
TABLA 1.1
Descripción: El anterior gráfico representa los tiempos para completar el armado de ciertos anaqueles de una fábrica de muebles de madera.
Interpretación: El tiempo que se repite con más frecuencias es el de 33.5 min, el mínimo tiempo es 32.8 y el máximo 34.4 minutos, que puede ser probablemente un dato atípico.
Requerimientos para realizar un gráfico:
RESUMEN ESTADÍSTICO
(para datos cuantitativos)
*Tomando en cuenta las características de los datos
Media
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
Mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
Moda
Es el valor de la variable que más se repite o el que tiene mayor frecuencia. Un conjunto puede tener más de una moda.
Percentiles
Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.
Ejercicio: En una fábrica de muebles se controló el tiempo en minutos, necesario para completar un trabajo de armado de ciertos anaqueles.
Elabore una tabla de distribución de frecuencias.
Resultado:
TABLA 1.1
Diagrama de Puntos
GRÁFICO 1.1
Interpretación: El tiempo que se repite con más frecuencias es el de 33.5 min, el mínimo tiempo es 32.8 y el máximo 34.4 minutos, que puede ser probablemente un dato atípico.
Requerimientos para realizar un gráfico:
- Número
- Título
- Título en los ejes
- Escalas adecuadas
- Descripción
- Interpretación
RESUMEN ESTADÍSTICO
(para datos cuantitativos)
*Tomando en cuenta las características de los datos
Media
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
Mediana
Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor.
Moda
Es el valor de la variable que más se repite o el que tiene mayor frecuencia. Un conjunto puede tener más de una moda.
Percentiles
Los percentiles son los 99 valores que dividen la serie de datos en 100 partes iguales.
Li es el límite inferior de la clase donde se encuentra el percentil.
N es la suma de las frecuencias absolutas.
Fi-1 es la frecuencia acumulada anterior a la clase del percentil.
ai es la amplitud de la clase.
Martes 08 de Noviembre del 2016
Clase#5
2. Medidas de Dispersión
1. Rango = ( Xmáx - Xmín )
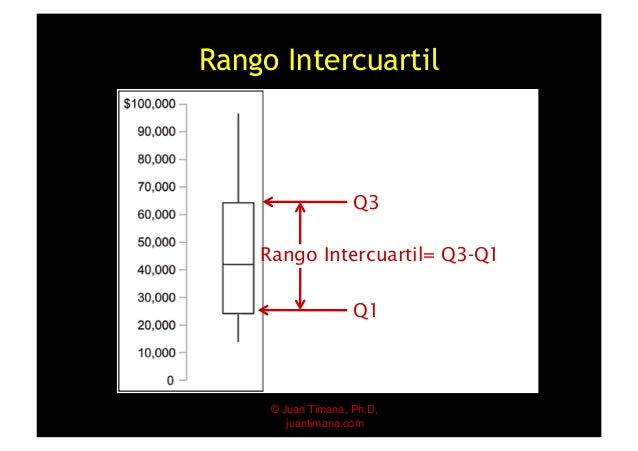
2. Rango Intercuartil ( RIQ )
RIQ = Q3-Q1
Es el rango que se encuentra entre el primer y el tercer cuartil
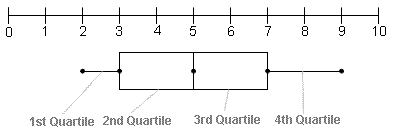
DIAGRAMA DE CAJAS (BIGOTES)
Se utiliza para visualizar la simetría de la distribución de datos y la posible presencia de datos atípicos. En cada espacio entre brazo-caja y caja-caja se encuentra el 25% de los datos.
DIVISIÓN EN INTERVALOS
Existe una fórmula Empírica propuesta
Donde:
k= es el número de intervalos recomendados
n= es el número de datos o el tamaño de la muestra
2. Medidas de Dispersión
1. Rango = ( Xmáx - Xmín )
2. Rango Intercuartil ( RIQ )
RIQ = Q3-Q1
Es el rango que se encuentra entre el primer y el tercer cuartil
DIAGRAMA DE CAJAS (BIGOTES)
Se utiliza para visualizar la simetría de la distribución de datos y la posible presencia de datos atípicos. En cada espacio entre brazo-caja y caja-caja se encuentra el 25% de los datos.
DIVISIÓN EN INTERVALOS
Existe una fórmula Empírica propuesta
k= 1+3.3*log(n)
k= es el número de intervalos recomendados
n= es el número de datos o el tamaño de la muestra
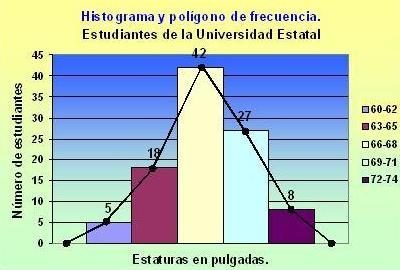
HISTOGRAMA
Para graficar el histograma se necesita la tabla de distribución de frecuencia de datos agrupados en intervalos o clases.
Se coloca en el eje OX los intervalos o clases y en el eje OY la frecuencia absoluta o frecuencia relativa.
EJEMPLO DE HISTOGRAMA
La línea que pasa por el punto medio, se llama POLÍGONO DE FRECUENCIA y se forma al unir las marcas de clase de cada intervalo
Datos Cuantitativos => HISTOGRAMA
Datos Cualitativos =>DIAGRAMA DE BARRAS; DIAGRAMA CIRCULA O PASTEL
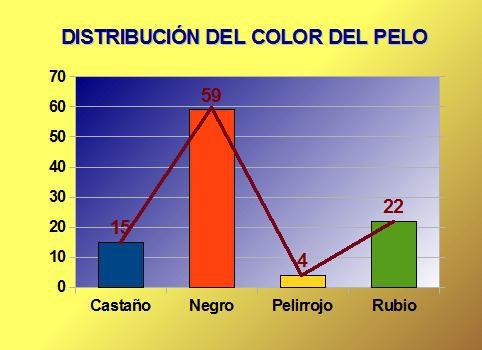
DIAGRAMA DE BARRAS
EJEMPLO DE DIAGRAMA DE BARRAS
DIAGRAMA CIRCULAR O PASTEL
EJEMPLO DE DIAGRAMA CIRCULAR
Viernes 11 de Noviembre del 2016
Clase#6
3. Varianza (s^2)
4. Desviación Estándar o Típica (s)
5. Coeficiente de Variación (Cv) (PEARSON)
3. Medidas de Forma:
1. Coeficiente de Asimetría (As)
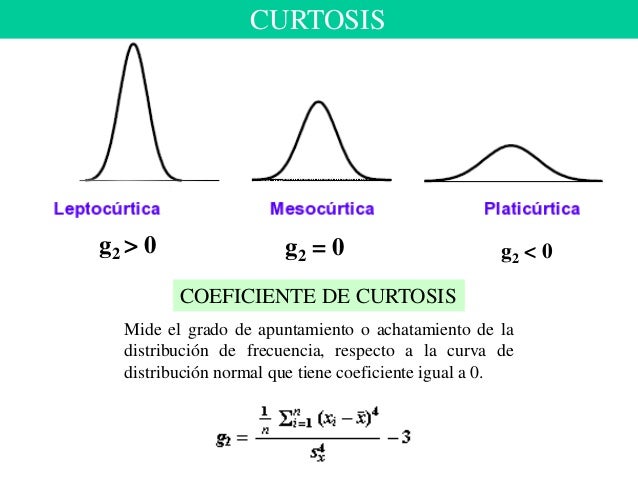
2. Coeficiente de Apuntamiento o curtosis (Ap)
REALIZACIÓN DE TRABAJO EN CLASE:
https://drive.google.com/open?id=14TNohLWqf5TXvN4YbY62-xEtB_f3TiTfDuqHJSKQVtU
4. Calcular la Covarianza
5. Calcular el coeficiente de correlación lineal
6. Construir las Matrices
Matriz de correlación
3. Varianza (s^2)
5. Coeficiente de Variación (Cv) (PEARSON)
1. Coeficiente de Asimetría (As)
2. Coeficiente de Apuntamiento o curtosis (Ap)
REALIZACIÓN DE TRABAJO EN CLASE:
https://drive.google.com/open?id=14TNohLWqf5TXvN4YbY62-xEtB_f3TiTfDuqHJSKQVtU
Martes 15 de Noviembre del 2016
Clase#7
REALIZACIÓN DE ACTIVIDAD (1-2) CORAZÓN
Viernes 18 de Noviembre del 2016
Clase#8
Muestras Bivariables
Para realizar el análisis estadístico de una muestra bivariable de datos cuantitativos, y de esta manera resolver si los datos tienen una relación entre ellos se hace el siguiente proceso:
1. Identificar las variables.
2. Realizar un diagrama de dispersión.
3. Realizar el análisis de la correlación.
4. Calcular la Covarianza
5. Calcular el coeficiente de correlación lineal
6. Construir las Matrices
Matriz varianza convarianza
Matriz de correlación
Martes 22 de Noviembre del 2016
Clase#9CAPÍTULO #2
PROBABILIDAD
Experimento: Es un procedimiento mediante el cual se trata de comprobar (confirmar o verificar) una o varias hipótesis relacionadas con un determinado fenómeno, mediante la manipulación y el estudio de las correlaciones de las variables que presumiblemente son su causa.
Ejemplos: Lanzar una Moneda, Sacar una carta, Lanzar un dado, etc.
Espacio Muestral: Es el conjunto de todos los posibles resultados de un experimento.
Ejemplos: {Cara, Sello} (al lanzar una moneda) {1,2,3,4,5,6} (Al lanzar un dado de 6 caras)
Todos los subconjuntos posibles de un espacio muestral se pueden determinar por:
La probabilidad de un evento es:
Sea el evento A
P(A) = k/n
- Donde k es los resultados favorables, y n es todos los resultados posbiles
REGLA DE LA SUMA
Sean los eventos A, B:
P(AUB) = P(A) + P(B) - P(A&B)
Viernes 25 de Noviembre del 2016
Clase#10
MÉTODOS DE CONTEO
Si hay n1 elecciones1 y n2 elecciones2, el número de operaciones posibles se encuentra como
(n1 * n2) = #opciones
o
(n1 * n2 * n3 * ... * nk) =#opciones
Permutaciones: (importa el orden), Si solo se cambia el orden de los elementos el número de
permutaciones posibles es igual a n!
Por diferentes subconjuntos la regla general queda:
CASOS ESPECIALES
Arreglo Circular: #Permutaciones = (n-1)!
Elementos Repetidos:
Combinaciones:
(Arreglos donde no importa el orden)
A continuación algunos videos con ejemplos y explicaciones.
Martes 29 de Noviembre del 2016
Clase#11
Probabilidad Condicional y Dependencia
Si se tiene enventos A y B:
Se dice que la probabilidad de que suceda el evento A, está condicionada a que previamente haya sucedido el evento B, nos permite definir eventos dependientes y se calcula:
Donde P(A/B) no es igual a P(B/A)
y
P(A) y P(B) no sean igual a 0
Ejemplos y explicaciones:





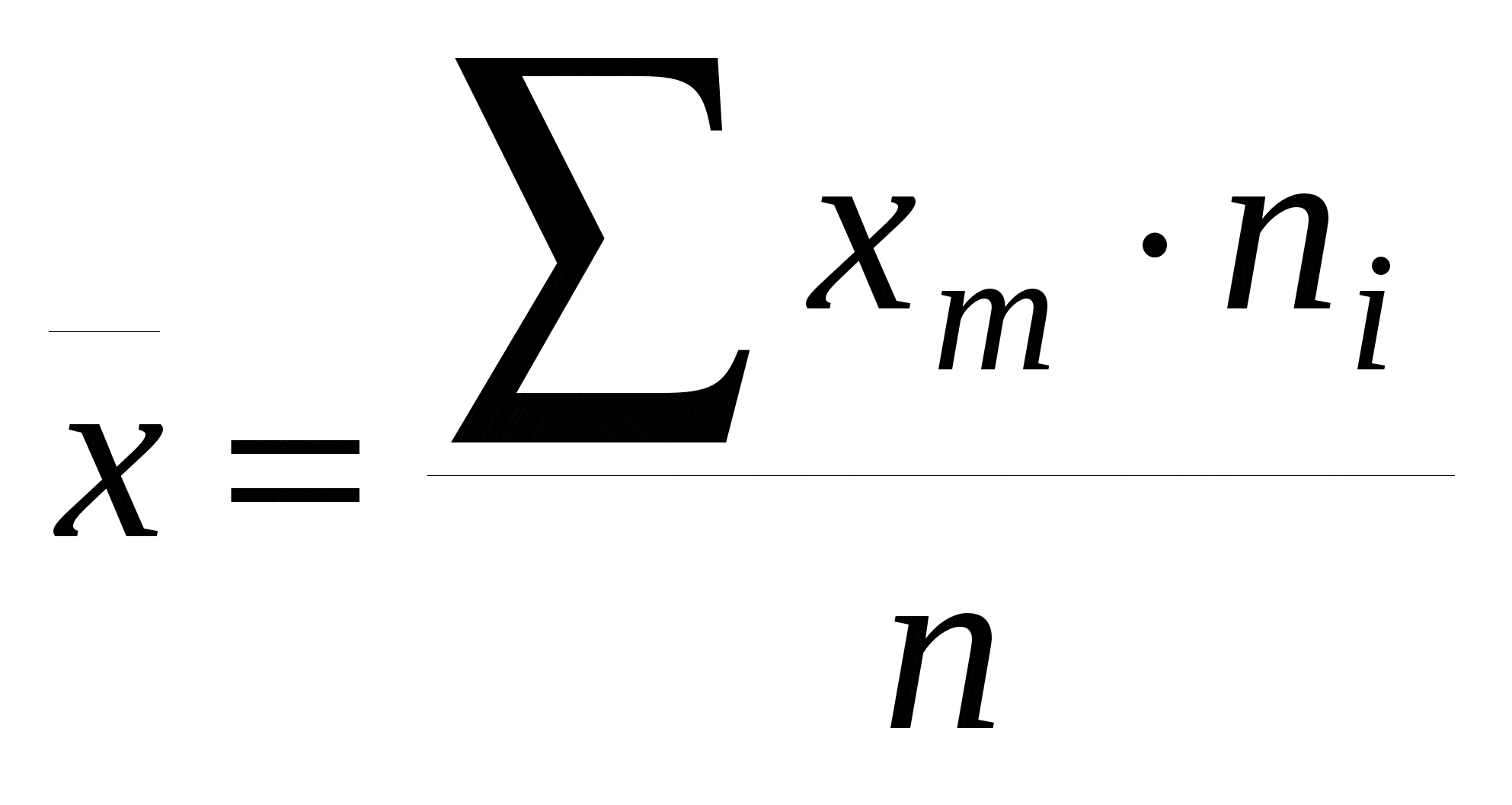
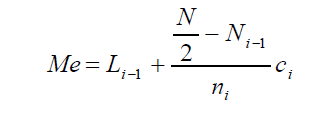



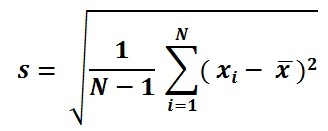





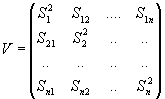





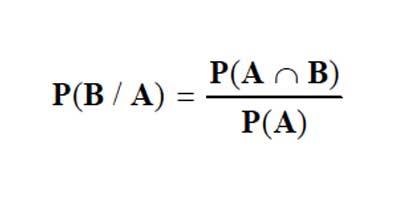

No hay comentarios.:
Publicar un comentario