Clase # 16
DISTRIBUCIÓN DE BERNOULLI
Es un experimento con solo 2 posibles resultados donde la probabilidad de éxito se denota con p y la de fracaso con q. Es una v.a.d
Éxito = 1
Fracaso =0
p = probabilidad de éxito
q= probabilidad de fracaso (1-p)
Esperanza : E(x) = p
Varianza: V(x) = pq
DISTRIBUCIÓN BINOMIAL
Cada experimento solo puede tener dos posibles resultados
* n= número de pruebas (finito)
* k = número de éxitos
* p = probabilidad de éxito
* q = probabilidad de fracaso
Esperanza = n*p
Varianza = n*p*q
MARTES 10 DE ENERO
Clase # 17
DISTRIBUCIÓN DE POISSON
P(x)= Probabilidad de que ocurran X éxitos, cuando el número de ocurrencia es landa.
λ= media o promedio éxitos por unidad de tiempo, área o producto
x= número de éxitos que se desea que ocurra
λ y t tienen que estar en la misma unidad de tiempo
Características:
- Sucesos independientes
- x es una variable aleatoria discreta con valores enteros positivos
- Se da dentro de un intevalo de tiempo
- Lambda es un valor constate positivo (esperanza)
- si n > 29 y p < 0.05 entonces:
λ= E(x) = V(x ) = n
DISTRIBUCIÓN GEOMÉTRICA
Características:
- se realizan n pruebas hasta obtener el primer éxito
- se pueden obtener únicamente dos resultados, éxito o fracaso
- pruebas idénticas e independientes entre si
- la probabilidad de éxito p se mantiene constante.
- la variable aleatoria discreta X representa el # de intentos hasta obtener el primer éxito
DISTRIBCIÓN BINOMIAL NEGATIVA
•La variable aleatoria sólo puede tomar dos valores (éxito o fracaso).
•Las pruebas son independientes entre sí.
•La probabilidad de éxito es p y se mantiene constante de
prueba en prueba
x: # de ensayos hasta incluir el r-ésimo "éxito".
p=Probabilidad de que ocurra un éxito.
q=1-p=Probabilidad de que sucedad un fracaso.
r= # de exitos.
VIERNES 17 DE ENERO
CLASE # 18
Una variable aleatoria X, que puede tomar un número infinito de vaores 1,2,....,n, cada uno de los cuales tiene la misma probabilidad de ocurrir, se dice que sigue una ley de distribucion uniforme discreta. Es decir,
P(x=k)=1/n, k=1,2,3,....,n.
Su esperanza es igual a E(x)=(n+1)/2 y su varianza V(x)=(n2 -1)/12
Sus caracteristicas son:
- La variable aleatoria toma cada uno de sus valores con idéntica probabilidad.
- La media de una variable aleatoria discreta uniforme, coincide con uno de los valores de la misma observados en el experimento.
- La varianza de una v,a,d no depende del número de valores que pueda tomar una variable.
P(x=k) = 1/n
E(x) = (n+1)/2
V(x) = (n^2 - 1)/12
DISTRIBUCIÓN HIPERGEOMÉTRICA
DISTRIBUCIÓN DE PROBABILIDAD UNIFORME CONTINUA
E(x) = (b+a)/2
V(x) = (b-a)^2 /12
MARTES 24 DE ENERO
DISTRIBUCIÓN DE GAUSS (DISTRIBUCIÓN NORMAL)
Es utilizada para describir el comportamiento aleatorio de muchos procesos que ocurren
La distribución viene dada por:
DISTRIBUCIÓN ESTÁNDAR
Para estandarizar los valores es necesario realizar el cambio:
El área bajo la curva representa la probabilidad a calcular.
EJEMPLOS:
VIERNES 27 DE ENERO
Clase # 19
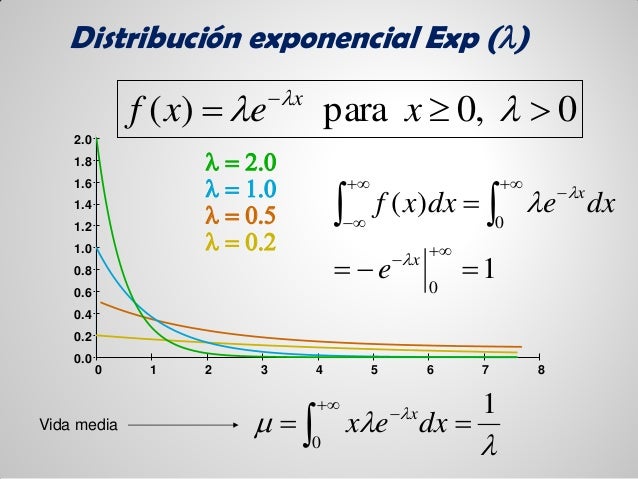
PROPIEDADES:
- No tiene memoria.
-Procesos independientes (Eventos que siguen un proceso Poisson)
E(x) = 1/λ
V(x) = 1/λ^2














No hay comentarios.:
Publicar un comentario